EEK! 6 months !
It’s not that I had nothing to write. On the contrary, I have a lot to post. I just didn’t found the time to write… Erm.. Let’s go with a 7 months old stuff.
While working on the tracker, I wanted to add some kind of “live” mode. The user could choose which sequence to play, modify it, control volume, add an effect etc… So I came with the idea to associate a command to a key combo.
Combos are detected by walking down a tree. Each time a button is pressed, we look at the current node and check if one of its children is associated to this button. If that’s the case, this child becomes the new current node. Otherwise there’s no matching combo and we reset the current node to the tree root. If the button pressed didn’t not changed for a certain amount of time (timeout), we check there’s a child corresponding to the current button. This way, we can detect combo containing a sequence like “press A button during t seconds”.
Let’s look at a simple example.

Mkit will successively return : DOWN – DOWN+RIGHT – RIGHT – 0 (aka nothing) – A
We have 0 because when you go from RIGHT to A, there’s a moment when you don’t press any button. And as we check keys every vsync, we necessary get 0 (unless if you are Superman on Redbull).
Consider we want to handle the following combos :

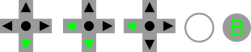

The combo tree is very similar to a lexical tree. A node can have 0 to N children but only one parent.
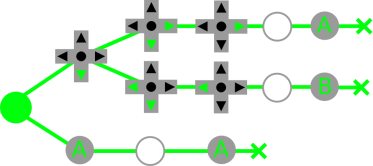
The tree is store in level-order with the longest path first. This means that you’ll have to be very careful and store node children by their depth. We have for our example :
Root – Down – A – Down+Right – Down+Left – Nothing – Left – Right – A – Nothing – Nothing – Leaf – A – B – Leaf – Leaf
In the current implement, the tree is stored in 2 arrays. The first one contains the index to first child of a node. And the second the key for each node.
combo_tree : 1, 3, 5, 6, 7, 8, 9, 10, 128 | 2, 11, 12, 128 | 0, 128 | 1 combo_keys: .db 255, JOY_DOWN, JOY_I, JOY_DOWN | JOY_RIGHT, JOY_DOWN | JOY_LEFT .db 0, JOY_RIGHT, JOY_LEFT, JOY_I, 0, 0, JOY_I, JOY_II
The root is always at index 0 and we associate the key value 255 to it.
The tree traversal algorithm is very simple. For a given node i, we know that its children are at indices j from combo_tree[i] to combo_tree[i+1]-1. And that we can reach them only if the current key is combo_key[j]. If the bit 7 of a value in the children list is set, this means that we have a transition a leaf. The remaining bits are used as an index to a jump table.
The traversal looks like this:
i // current node index
for(j=combo_tree[i]; j
If you have any question, feel free to leave a comment or go and join the [PCEdev Forum].
Talking about web stuff, I finally updated the gallery. Hurray!


