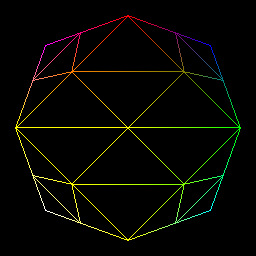
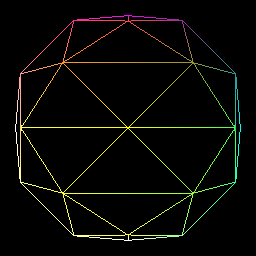
I recently played with median cut quantization. Like octree quantization, color space is viewed as a 3D space. But it uses a top-bottom approach. We start with a box containing all the image colors and then we split it into 2 smaller boxes along its longest side until the number of boxes is equal to the number of desired colors. The child boxes are then shrunk to enclose their color subset. Each color in the palette is then the mean of the colors contained in each box.
I used stl priority queue to store the boxes and get the box with the longest side. As each new box contains half of its parent color. The first subset contains all the colors where the component along the split axis is inferior to the median. And on the other hand, the second subset color component along the split axis are greater than the median. For this i use the nth_element function.
I should have used them for the octree quantization…
Talking about octree, i put all the image colors into one in order to easily map them to the palette.
The result is quite good with the sorcerian images.
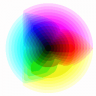
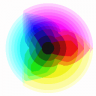
Here’s the RGB color wheel. The error is very important for low color count 🙁
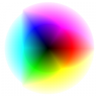 |
 |
| truecolor | 256 |
 |
 |
| 128 | 64 |
 |
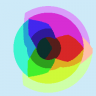 |
| 32 | 16 |
I tried to solve this problem by spliting the box along the axis with the highest variance. But the result is not that great.
Anyway! Grab the sources here.